Feature scaling , variables and distance between points

* Created by Ramses Alexander Coraspe Valdez

* Created on september 4, 2019

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math

raw_data = {'x1': [0.15, -0.1, 0, -0.25, 0.05],
'x2': [3500, 3400, 4000, 3900, 3200],
'y': [8, 5, 3, 1, 7]}
df = pd.DataFrame(raw_data)
df

	x1	x2	y
0	0.15	3500	8
1	-0.10	3400	5
2	0.00	4000	3
3	-0.25	3900	1
4	0.05	3200	7

plt.figure(figsize=(10, 7))
plt.scatter(df.x1,df.x2, label="Without scaling", color='blue')

plt.grid(True, alpha=0.6)
plt.title("Scatter", fontsize=20)
plt.xlabel("x1", fontsize=20) 
plt.ylabel("x2", fontsize=20) 
plt.legend()
plt.show()

def stddev(c):   
    v = 0
    mn = round(sum(c),2)/len(c)    
    for i in range(len(c)):
        v += (c[i]-mn)**2
    v /= len(c)
    return math.sqrt(v)

1.a) Scaling by normalization

def scalingByNormalization(c):
  newc = [None] * len(c)
  mean = round(sum(c),2)/len(c)
  sdev = stddev(c)  
  for i in range(len(c)):
    newc[i] = (c[i] - mean)/ sdev
    
  return newc      

nx1= scalingByNormalization(df.x1)
nx2= scalingByNormalization(df.x2)

1.b) Scaling by range

def scalingByRange(c):
  newc = [None] * len(c)
  mean = round(sum(c),2)/len(c)
  r = max(c)- min(c)
  for i in range(len(c)):
    newc[i] = (c[i] - mean)/ r
    
  return newc

mx1= scalingByRange(df.x1)
mx2= scalingByRange(df.x2)

plt.figure(figsize=(10, 7))
plt.scatter( nx1, nx2 ,label="Feature scaling by Normalization", color='orange')
plt.scatter(mx1, mx2 ,label="Feature scaling by range", color='green')


plt.grid(True, alpha=0.6)
plt.title("Scatter", fontsize=20)
plt.xlabel("x1", fontsize=20) 
plt.ylabel("x2", fontsize=20) 
plt.legend()
plt.show()

1.c) Scaling between range

def scalingBetweenRange(c, r1, r2):
  newc = [None] * len(c)
  
  for i in range(len(c)):    
    newc[i] = ((r2-r1)* ((c[i] - min(c))/(max(c)-min(c)))) + r1    
    
  return newc

ny= scalingBetweenRange(df.y,-10, 20)

df2 = pd.DataFrame(list(zip(nx1, nx2, mx1, mx2, ny)), 
               columns =['x1N', 'x2N', 'x1R', 'x2R', 'ny']) 
df2

	x1N	x2N	x1R	x2R	ny
0	1.319824	-0.329690	0.450	-0.125	20.000000
1	-0.513265	-0.659380	-0.175	-0.250	7.142857
2	0.219971	1.318761	0.075	0.500	-1.428571
3	-1.613118	0.989071	-0.550	0.375	-10.000000
4	0.586588	-1.318761	0.200	-0.500	15.714286

2.a) Euclidean distance

def euclidian(c1, c2):
	d=0
	for i in range(len(c1)):
		d += math.pow(c2[i] - c1[i], 2)
	return math.sqrt(d)

v1 = [2, 1]
v2 = [3, 4]
print(euclidian(v1, v2))

3.1622776601683795

2.b) Manhattan distance

def manhattan(c1, c2):
	d=0
	for i in range(len(c1)):
		d += abs(c1[i] - c2[i])
	return d

v1 = [2, 3]
v2 = [1, 4]
print(manhattan(v1,v2))

2

2.c) Chebyshev distance

def Chebyshev(c1, c2):  
  subtractions = [None] * len(c1)
  for i in range(len(c1)):
    subtractions[i] = abs(c2[i] - c1[i])
  
  return max(subtractions)

v1 = [2, 1]
v2 = [3, 4]
print(Chebyshev(v1, v2))

3

2.d) Minkowski distance

def Minkowski(c1,c2, p):
  pp = 1/p
  d=0
  for i in range(len(c1)):
    d +=  math.pow(abs(c1[i] - c2[i]),p)
         
  return math.pow(d, pp)     

v1 = [2, 1]
v2 = [3, 4]
print(Minkowski(v1,v2,0.7))

5.168695137549193

3. Suppose you want to apply the multiple linear regression method to a database whose variables or factors are shown in the image below. Let's also assume that at the moment only the following variables will be used to build the model:

• ### Independent variables: season, hour, workingday, windspeed
• ### Dependent variable: registered

3.a) Indicate what type of variable each one is: categorical or numerical. If it is numerical, so indicates whether it is discrete or continuous.

1. Categorical: Season, workingday
2. Numerical: registered(discrete), hour(discrete), windspeed(continuous)

3.b) In the case of categorical variables, indicate the dummies variables that you believe should be introduced to the model, indicating the base case of each of these dummy variables, or if you decided not to use base case and instead add a additional dummy variable. The base case is the variable that is considered in the model when all other dummy variables in that case are zero.

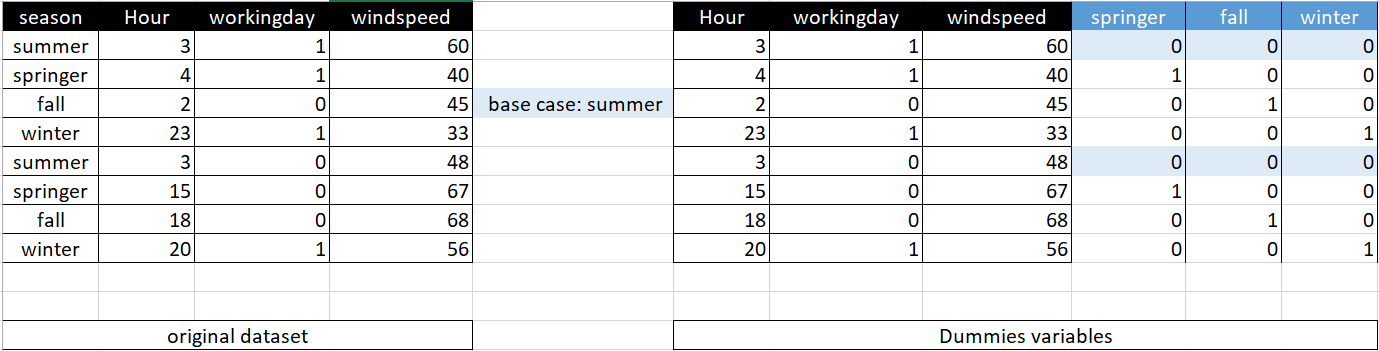
3.c) How many dummy variables were added? It indicates how the symbolic representation of the multiple linear regression model would look like when all independent, dummy or non-dummy variables are included.

• ### y= Bo + B1hour + B2workingday + B3windspeed + D1springer + D2fall + D3winter + E