Ramses Alexander Coraspe Valdez
Computer vision and Deep Learning homeworks
This repository contains information on the basic techniques and algorithms used in computer image processing, in addition to some projects related to pattern recognition using deep learning.
1. Image processing - Image transformations

1. Transformar a una imagen de grises usando la transformación ponderada.
La funciòn recibe una imagen en 24 bits (RGB) y retorna una imagen en la escala de grises en 8 bits
def TransformacionPonderada(list24bits):
return [round((0.29894 * list24bits[i][0]) +
(0.58704 * list24bits[i][1]) +
(0.11402 * list24bits[i][2]))
for i in range(len(list24bits))]

2. Transformarla a una imagen de grises con el promedio aritmético.
La funcion recibe una imagen en 24 bits (RGB) y retorna una imagen en la escala de grises en 8 bits
def TransformacionPromedioAritmetico(list24bits):
return [((list24bits[i][0]) +
(list24bits[i][1]) +
(list24bits[i][2]) /3)
for i in range(len(list24bits))]

3. A partir de la imagen de grises ponderada, realizar las siguientes transformaciones:
3.1. Aplicarle la transformación negativa.
La funcion recibe una imagen en 8 bits y retorna una imagen negativa
def TransformacionNegativa(list8bits):
return [(255 - list8bits[i])
for i in range(len(list8bits))]

3.2. Binarizarla con un umbral de 150 y la función: t(x) = 0, x<= 150; t(x)=255, x>150.
La funcion recibe una imagen en 8 bits y retorna una imagen binarizada usando un umbral de 150
def TransformacionBinarizadaUmbral(list8bits, umbral):
return [ (0 if list8bits[i]<= umbral else 255 )
for i in range(len(list8bits))]

3.3 Aplicar la transformación de raíz cuadrada y escalarla en (0, 255).
La funcion recibe una imagen en 8 bits, se calcula la raiz cuadrada del valor de cada pixel y el resultado final se escala
def escalar(list8bits):
mi = min(list8bits)
ma = max(list8bits)
newlist = [ ((255) /(ma - mi)) * (list8bits[i] - mi)
for i in range(len(list8bits))]
return newlist
def TransformacionRaizCuadrada(list8bits):
return [( math.sqrt(list8bits[i]))
for i in range(len(list8bits))]
TRC = escalar(TransformacionRaizCuadrada(TP))

3.4 Aplicar la transformación de potencia al cubo y escalarla en (0, 255).
La funcion recibe una imagen en 8 bits, se calcula la la potencia al cubo del valor de cada pixel y el resultado final se escala
def escalar(list8bits):
mi = min(list8bits)
ma = max(list8bits)
newlist = [ ((255) /(ma - mi)) * (list8bits[i] - mi)
for i in range(len(list8bits))]
return newlist
def TransformacionPotencia(list8bits, potencia):
return [(list8bits[i]**potencia)
for i in range(len(list8bits))]
TPC = escalar(TransformacionPotencia(TP, 3))

Código
import math
from PIL import Image
def escalar(list8bits):
mi = min(list8bits)
ma = max(list8bits)
newlist = [ ((255) /(ma - mi)) * (list8bits[i] - mi)
for i in range(len(list8bits))]
return newlist
def TransformacionPonderada(list24bits):
return [round((0.29894 * list24bits[i][0]) +
(0.58704 * list24bits[i][1]) +
(0.11402 * list24bits[i][2]))
for i in range(len(list24bits))]
def TransformacionPromedioAritmetico(list24bits):
return [((list24bits[i][0]) +
(list24bits[i][1]) +
(list24bits[i][2]) /3)
for i in range(len(list24bits))]
def TransformacionNegativa(list8bits):
return [(255 - list8bits[i])
for i in range(len(list8bits))]
def TransformacionBinarizadaUmbral(list8bits, umbral):
return [ (0 if list8bits[i]<= umbral else 255 )
for i in range(len(list8bits))]
def TransformacionRaizCuadrada(list8bits):
return [( math.sqrt(list8bits[i]))
for i in range(len(list8bits))]
def TransformacionPotencia(list8bits, potencia):
return [(list8bits[i]**potencia)
for i in range(len(list8bits))]
def convertirImagen(size, list8bits, filename):
newimage = Image.new('L', size)
newimage.putdata(list8bits)
newimage.save(filename)
newimage.close()
return 1
imagenColor = Image.open('C:/ejemplos/baboon.png')
Matrix = list(imagenColor.getdata())
TP = TransformacionPonderada(Matrix)
convertirImagen(imagenColor.size,TP,'C:/ejemplos/baboon_TP.png')
TPA = TransformacionPromedioAritmetico(Matrix)
convertirImagen(imagenColor.size,TPA,'C:/ejemplos/baboon_TPA.png')
TN = TransformacionNegativa(TP);
convertirImagen(imagenColor.size,TN,'C:/ejemplos/baboon_TN.png')
TB = TransformacionBinarizadaUmbral(TP, 150)
convertirImagen(imagenColor.size,TB,'C:/ejemplos/baboon_TB.png')
TRC = escalar(TransformacionRaizCuadrada(TP))
convertirImagen(imagenColor.size,TRC,'C:/ejemplos/baboon_TRC.png')
TPC = escalar(TransformacionPotencia(TP, 3))
convertirImagen(imagenColor.size,TPC,'C:/ejemplos/baboon_TPC.png')
imagenColor.close()
2. Edge Detection
1. Obtener la correlación cruzada H ⨂ w, de la imagen con dicho kernel, y obtener la convolucion H * w
def correlacion_cruzada(i, k):
return sn.correlate2d(i,k,'same',boundary='wrap', fillvalue=0)
def convolucion(i, k):
return sn.convolve2d(i,k,'same',boundary='wrap', fillvalue=0)
def rotar(a, g):
if g == 0:
return a
elif g > 0:
return rotar(list(zip(*a[::-1])), g-90)
else:
return rotar(list(zip(*a)[::-1]), g+90)
#kernel w
w = np.array(([-10,-10, 0],
[-10, 0, 10],
[ 0, 10, 10]),
np.float32)
#matriz h
h = np.array(([10, 20, 0, 30, 30],
[20, 0, 10, 20, 0],
[10, 0, 40, 10, 10],
[20, 40, 0, 30, 10],
[0, 10, 40, 20, 0]),
np.float32)
print("** Primer ejercicio ** ")
cr = correlacion_cruzada(h,w)
print("Correlacion cruzada:")
print(cr)
cv = convolucion(h,np.array(rotar(w,180),np.float32))
print("Convolucion:")
print(cv)
2. Obtener las convoluciones HQ , Hq y (H * q) qt, q= [-1,3,-1]
def convolucion(i, k):
return sn.convolve2d(i,k,'same',boundary='wrap', fillvalue=0)
print("** Segundo ejercicio ** ")
# Vector q
q = np.array(([-1, 3, -1]), np.float32)
print("q:")
# Traspuesta de q = qt
qt = q.reshape((-1,1))
print("qt:")
#Q = qt*q
Q= np.outer(q, qt);
print(Q)
crQ = convolucion(h,Q)
print("Convolucion h * Q:")
print(crQ)
crq = convolucion(h, q[None,:])
print("Convolucion h * q:")
print(crq)
crqt = convolucion(crq, qt)
print("Convolucion (h * q)qt:")
print(crqt)
3. Usando la herramienta que mejor consideres, utiliza el operador Sobel de dicha librería para hacer la práctica que se indica en la diapositiva
def contornos_sobel(filename):
imyo = Image.open(filename);
imyoo = np.array(Image.open(filename))
##sobel
img_sobelx = cv2.Sobel(imyoo,cv2.CV_8U,1,0,None,ksize=3,scale=1,delta=0)
img_sobely = cv2.Sobel(imyoo,cv2.CV_8U,0,1,None,ksize=3,scale=1,delta=0)
img_total = imyoo + img_sobelx + img_sobely
scipy.misc.imsave("imyogray_sobelx.jpg", img_sobelx)
scipy.misc.imsave("imyogray_sobely.jpg", img_sobely)
scipy.misc.imsave("imyogray_sobel.jpg", img_total )
images = np.array([])
images = np.append(images, imyoo)
images = np.append(images, img_sobelx)
images = np.append(images, img_sobely)
images = np.append(images, img_total)
imyo.close()
return images
print("** Tercer ejercicio ** ")
contornos = contornos_sobel('yo.jpg')



4. Este ejercicio debe usar la imagen en tono de grises de panda.png, la cual Usando la información del gradiente con el operador derivada que creas más conveniente (ver archivo 02_Transformaciones_Varias.pdf, diapositiva 36), dibujar en la imagen los vectores gradiente ortogonales a como se muestran en las imágenes de las diapositivas 36 y 37 del archivo mencionado. Para calcular y aproximar el gradiente puedes utilizar cualquiera de los kernels derivada que desees para obtener las parciales con X y Y. Sin embargo, la magnitud de todos ellos darle un valor constante a tu elección. Además, para una mejor visualización de los vectores gradientes, puedes dibujar solamente un porcentaje de dichos vectores gradientes y solo aquellos que tengan las magnitudes más significativas.
def vectores_gradientes(filename):
#leo la imagen y obtengo una en gris para aplicar el sobel
img = Image.open(filename);
im = np.array(Image.open(filename).convert('L'))
# obtengo las dimensiones de las columnas y filas
Ro = np.arange(0,im.shape[0]-1)
Co = np.arange(0,im.shape[1]-1)
#obtengo el filtro sobel para las lineas horizontales
imx = np.zeros(im.shape)
filters.sobel(im,1,imx)
#obtengo el filtro sobel para las lineas verticales
imy = np.zeros(im.shape)
filters.sobel(im,0,imy)
#obtengo las magnitudes y los angulos de todos los vectores, usando las derivadas de sobel
mag, angle = cv2.cartToPolar(imx, imy, angleInDegrees=True)
#obtego el promedio de las magnitudes
alphavectors = np.mean(mag)
#elimino vectores no relevantes que tengan una magnitud menor al promedio
for x in range(0, mag.shape[0]):
for y in range(0, mag.shape[1]):
if mag[x, y] <= alphavectors:
imx[x, y] = None
imy[x, y] = None
x, y = np.meshgrid(Ro, Co)
skip = (slice(None, None,4), slice(None, None, 4))
fig, ax = plt.subplots()
imi = ax.imshow(img)
ax.quiver(x[skip], y[skip], imx[skip], imy[skip], angles='xy', scale_units='xy', scale=25, pivot='mid',color='g')
plt.show()
print("** Cuarto ejercicio ** ")
vectores_gradientes("panda.jpg")


Código
import cv2
import numpy as np
import scipy.signal as sn
import scipy.misc
from matplotlib import pyplot as plt
from PIL import Image
from scipy.ndimage import filters
def magnitud_Constante(v):
if(v<0): return -100
else: return 100
def correlacion_cruzada(i, k):
return sn.correlate2d(i,k,'same',boundary='wrap', fillvalue=0)
def convolucion(i, k):
return sn.convolve2d(i,k,'same',boundary='wrap', fillvalue=0)
def rotar(a, g):
if g == 0:
return a
elif g > 0:
return rotar(list(zip(*a[::-1])), g-90)
else:
return rotar(list(zip(*a)[::-1]), g+90)
def vectores_gradientes(filename):
#leo la imagen y obtengo una en gris para aplicar el sobel
img = Image.open(filename);
im = np.array(Image.open(filename).convert('L'))
# obtengo las dimensiones de las columnas y filas
Ro = np.arange(0,im.shape[0]-1)
Co = np.arange(0,im.shape[1]-1)
#obtengo el filtro sobel para las lineas horizontales
imx = np.zeros(im.shape)
filters.sobel(im,1,imx)
#obtengo el filtro sobel para las lineas verticales
imy = np.zeros(im.shape)
filters.sobel(im,0,imy)
#obtengo las magnitudes y los angulos de todos los vectores, usando las derivadas de sobel
mag, angle = cv2.cartToPolar(imx, imy, angleInDegrees=True)
#obtego el promedio de las magnitudes
alphavectors = np.mean(mag)
#elimino vectores no relevantes que tengan una magnitud menor al promedio
for x in range(0, mag.shape[0]):
for y in range(0, mag.shape[1]):
if mag[x, y] <= alphavectors:
imx[x, y] = None
imy[x, y] = None
x, y = np.meshgrid(Ro, Co)
skip = (slice(None, None,4), slice(None, None, 4))
fig, ax = plt.subplots()
imi = ax.imshow(img)
ax.quiver(x[skip], y[skip], imx[skip], imy[skip], angles='xy', scale_units='xy', scale=25, pivot='mid',color='g')
plt.show()
def contornos_sobel(filename):
imyo = Image.open(filename);
imyoo = np.array(Image.open(filename))
##sobel
img_sobelx = cv2.Sobel(imyoo,cv2.CV_8U,1,0,None,ksize=3,scale=1,delta=0)
img_sobely = cv2.Sobel(imyoo,cv2.CV_8U,0,1,None,ksize=3,scale=1,delta=0)
img_total = imyoo + img_sobelx + img_sobely
scipy.misc.imsave("imyogray_sobelx.jpg", img_sobelx)
scipy.misc.imsave("imyogray_sobely.jpg", img_sobely)
scipy.misc.imsave("imyogray_sobel.jpg", img_total )
images = np.array([])
images = np.append(images, imyoo)
images = np.append(images, img_sobelx)
images = np.append(images, img_sobely)
images = np.append(images, img_total)
imyo.close()
return images
def main():
#kernel w
w = np.array(([-10,-10, 0],
[-10, 0, 10],
[ 0, 10, 10]),
np.float32)
#matriz h
h = np.array(([10, 20, 0, 30, 30],
[20, 0, 10, 20, 0],
[10, 0, 40, 10, 10],
[20, 40, 0, 30, 10],
[0, 10, 40, 20, 0]),
np.float32)
print("** Primer ejercicio ** ")
cr = correlacion_cruzada(h,w)
print("Correlacion cruzada:")
print(cr)
cv = convolucion(h,np.array(rotar(w,180),np.float32))
print("Convolucion:")
print(cv)
print("** Segundo ejercicio ** ")
# Vector q
q = np.array(([-1, 3, -1]), np.float32)
print("q:")
# Traspuesta de q = qt
qt = q.reshape((-1,1))
print("qt:")
#Q = qt*q
Q= np.outer(q, qt);
print(Q)
crQ = convolucion(h,Q)
print("Convolucion h * Q:")
print(crQ)
crq = convolucion(h, q[None,:])
print("Convolucion h * q:")
print(crq)
crqt = convolucion(crq, qt)
print("Convolucion (h * q)qt:")
print(crqt)
print("** Tercer ejercicio ** ")
contornos = contornos_sobel('yo.jpg')
print("** Cuarto ejercicio ** ")
vectores_gradientes("panda.jpg")
if __name__ == '__main__':
main()
3. Counting objects
Imagen original para las pruebas

Metodología
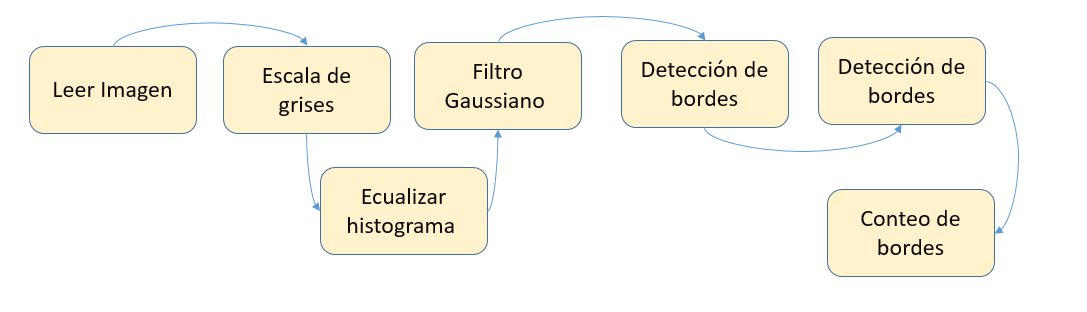
1. Leer imagen
def LeerImagen(l):
Imagen = cv2.imread(l)
return Imagen, Imagen.copy()
2. Transformar la imagen a escala de grises, ecualizar el histograma y filtrar el ruido
def PreprocessImage(i):
return cv2.GaussianBlur(cv2.equalizeHist(cv2.cvtColor(i, cv2.COLOR_BGR2GRAY)), (5,5),0)
3. Deteccion de bordes usando Canny
def DetectarContornos(i, min, max):
ImagenBordes = cv2.Canny(i, min, max)
contornos,_ = cv2.findContours(ImagenBordes.copy(), cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
return ImagenBordes, contornos
4. Conteo de bordes
def DibujarContornos(c):
global ImagenContornos
i = 0
for cn in c:
cv2.drawContours(ImagenContornos, cn, -1, (57,255,20),2)
x,y,w,h = cv2.boundingRect(cn)
cv2.putText(ImagenContornos, str(i+1), (x, y-5), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (57, 255, 20), lineType=cv2.LINE_AA)
i=i+1
return i
4. Resultados

Código
import numpy as np
import cv2
from matplotlib import pyplot as plt
ImagenContornos= None
def LeerImagen(l):
Imagen = cv2.imread(l)
return Imagen, Imagen.copy()
def PreprocessImage(i):
return cv2.GaussianBlur(cv2.equalizeHist(cv2.cvtColor(i, cv2.COLOR_BGR2GRAY)), (5,5),0)
def DetectarContornos(i, min, max):
ImagenBordes = cv2.Canny(i, min, max)
contornos,_ = cv2.findContours(ImagenBordes.copy(), cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
return ImagenBordes, contornos
def DibujarContornos(c):
global ImagenContornos
i = 0
for cn in c:
cv2.drawContours(ImagenContornos, cn, -1, (57,255,20),2)
x,y,w,h = cv2.boundingRect(cn)
cv2.putText(ImagenContornos, str(i+1), (x, y-5), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (57, 255, 20), lineType=cv2.LINE_AA)
i=i+1
return i
def Plotear(t,im,s, n):
for i in range(n):
plt.subplot(2, 2, i+1)
plt.title(t[i])
if(s[i]):
plt.imshow(im[i], cmap='gray',vmin=0,vmax=255)
else:
plt.imshow(cv2.cvtColor(im[i], cv2.COLOR_BGR2RGB))
plt.xticks([])
plt.yticks([])
plt.show()
def ContarMonedas(location):
global ImagenContornos
Imagen, ImagenContornos = LeerImagen(location)
ImagenGauss = PreprocessImage(Imagen)
ImagenBordes,contornos= DetectarContornos(ImagenGauss, 50, 300)
i = DibujarContornos(contornos)
Titulos = ['Original', 'Gaussiana', 'Bordes de la imagen', 'Imagen Final: ' + str(i) + ' monedas']
Imagenes = [Imagen, ImagenGauss, ImagenBordes, ImagenContornos]
Types = [0, 1, 0, 0]
Plotear(Titulos, Imagenes, Types, 4)
def main():
ContarMonedas('monedas.png')
if __name__ == '__main__':
main()
4. Morphological Operations and Geometric Transformations
Imagen para las pruebas



1. Obtener un esqueleto
def ObtenerEsqueleto(imagename, inverse):
global EE
fin = False
Imagen = Binarize(cv2.GaussianBlur(LeerImagen(imagename), (61,61),0),inverse)[1]
#cv2.imshow("e", Imagen)
#cv2.waitKey(0)
tamaño = np.size(Imagen)
esqueleto = np.zeros(Imagen.shape, np.uint8)
while(not fin):
e= cv2.erode(Imagen, EE)
d= cv2.dilate(e,EE)
r= cv2.subtract(Imagen, d)
esqueleto= cv2.bitwise_or(esqueleto, r)
Imagen = e.copy()
if ((tamaño-cv2.countNonZero(Imagen))==tamaño):
fin= True
return esqueleto
3. Rotacion de la imagen
def RotarImagen(imagen, angulo, punto):
i = LeerImagen(imagen)
tamaño = np.size(i)
rotada = np.zeros(i.shape, np.uint8)
R = [[math.cos(math.radians(angulo)), -math.sin(math.radians(angulo)), 0],
[math.sin(math.radians(angulo)), math.cos(math.radians(angulo)), 0],
[0, 0, 1]]
T = [[1, 0, -punto[0]],
[0, 1, -punto[1]],
[0, 0, 1]]
T_i = np.linalg.inv(T)
A = np.dot(T_i, R)
A = np.dot(A, T)
F = np.zeros(shape=(3,1))
for x in range(0, i.shape[0]):
for y in range(0, i.shape[1]):
p = [[x],[y],[1]]
F = np.dot(A, p).astype(int)
try:
rotada[F[[0,1]][0],F[[0,1]][1]] = i[x,y]
except:
error= True
return rotada
4. Resultados
Código
import math
import numpy as np
import cv2
from matplotlib import pyplot as plt
EE = cv2.getStructuringElement(cv2.MORPH_CROSS,(3,3))
def LeerImagen(l):
return cv2.imread(l,0)
def Plotear(t,im,s, n):
for i in range(n):
plt.subplot(1, 3, i+1)
plt.title(t[i])
if(s[i]):
plt.imshow(im[i], cmap='gray',vmin=0,vmax=255)
else:
plt.imshow(cv2.cvtColor(im[i], cv2.COLOR_BGR2RGB))
plt.xticks([])
plt.yticks([])
plt.show()
def Binarize(i,inverse):
t = 0
if inverse:
t= 1
return cv2.threshold(i,200, 255, t)
def ObtenerEsqueleto(imagename, inverse):
global EE
fin = False
Imagen = Binarize(cv2.GaussianBlur(LeerImagen(imagename), (61,61),0),inverse)[1]
#cv2.imshow("e", Imagen)
#cv2.waitKey(0)
tamaño = np.size(Imagen)
esqueleto = np.zeros(Imagen.shape, np.uint8)
while(not fin):
e= cv2.erode(Imagen, EE)
d= cv2.dilate(e,EE)
r= cv2.subtract(Imagen, d)
esqueleto= cv2.bitwise_or(esqueleto, r)
Imagen = e.copy()
if ((tamaño-cv2.countNonZero(Imagen))==tamaño):
fin= True
return esqueleto
def RotarImagen(imagen, angulo, punto):
i = LeerImagen(imagen)
tamaño = np.size(i)
rotada = np.zeros(i.shape, np.uint8)
R = [[math.cos(math.radians(angulo)), -math.sin(math.radians(angulo)), 0],
[math.sin(math.radians(angulo)), math.cos(math.radians(angulo)), 0],
[0, 0, 1]]
T = [[1, 0, -punto[0]],
[0, 1, -punto[1]],
[0, 0, 1]]
T_i = np.linalg.inv(T)
A = np.dot(T_i, R)
A = np.dot(A, T)
F = np.zeros(shape=(3,1))
for x in range(0, i.shape[0]):
for y in range(0, i.shape[1]):
p = [[x],[y],[1]]
F = np.dot(A, p).astype(int)
try:
rotada[F[[0,1]][0],F[[0,1]][1]] = i[x,y]
except:
error= True
return rotada
def main():
Letras= ObtenerEsqueleto('letras.png', False)
Caballo= ObtenerEsqueleto('caballo.png', True)
punto = [180, 270]
Minerva = RotarImagen('minerva.png', 35, punto)
Titulos = ['Letras esqueleto', "Caballo esqueleto", "Minerva"]
Imagenes = [Letras, Caballo, Minerva ]
Types = [1, 1, 1]
Plotear(Titulos, Imagenes, Types, 3)
if __name__ == '__main__':
main()
5. Projective Transformation
Imagen para las pruebas

Seleccionar primero los 4 puntos de la imagen origen
Seleccionar despues los 4 puntos de la imagen destino

4. Resultados

Código
import numpy as np
from scipy import misc
import cv2
from matplotlib import pyplot as plt
from PIL import Image
color_point = (0,0,255)
def mouse_handler(event, x, y, flags, data) :
if event == cv2.EVENT_LBUTTONDOWN :
cv2.circle(data['im'], (x,y),3, color_point, 5, 16);
cv2.imshow("Image", data['im']);
if len(data['points']) < 4 :
data['points'].append([x,y])
def getXYMouse(im, color):
global color_point
color_point = color
data = {}
data['im'] = im.copy()
data['points'] = []
cv2.imshow("Image",im)
cv2.setMouseCallback("Image", mouse_handler, data)
cv2.waitKey(0)
points = np.vstack(data['points']).astype(int)
return points
def LeerImagen(l):
return cv2.imread(l)
def TransformacionProyectiva(i, o, d):
im = misc.imread(i)
if(len(o)<1 or len(d)<1):
cv2.imshow("Image", im)
o = obtenerCoordenada(im,(0,0,255))
print(o)
d = obtenerCoordenada(im,(255,0,0))
print(d)
MAT = np.zeros((8,9))
for ite in range(4):
MAT[ite*2,:] = [ o[ite][1], o[ite][0], 1,
0, 0, 0,
-d[ite][1]*o[ite][1], -d[ite][1]*o[ite][0], -d[ite][1] ]
MAT[ite*2+1,:] = [0, 0, 0,
o[ite][1], o[ite][0], 1,
-d[ite][0]*o[ite][1], -d[ite][0]*o[ite][0], -d[ite][0] ]
mx=[];
my=[];
[Z,Y,X]=np.linalg.svd(MAT)
mat = X[-1,:]
matH = np.reshape(mat,(3,3))
txy = np.array([[1],[1],[1]])
txytemporal = np.dot(matH,txy)
mx.append(txytemporal[0]/txytemporal[2])
my.append(txytemporal[1]/txytemporal[2])
txy = np.array([[im.shape[1]],[1],[1]])
txytemporal = np.dot(matH,txy)
mx.append(txytemporal[0]/txytemporal[2])
my.append(txytemporal[1]/txytemporal[2])
txy = np.array([[1],[im.shape[0]],[1]])
txytemporal = np.dot(matH,txy)
mx.append(txytemporal[0]/txytemporal[2])
my.append(txytemporal[1]/txytemporal[2])
txy = np.array([[im.shape[1]],[im.shape[0]],[1]])
txytemporal = np.dot(matH,txy)
mx.append(txytemporal[0]/txytemporal[2])
my.append(txytemporal[1]/txytemporal[2])
XX1 = int(np.min(mx))
XX2 = int(np.max(mx))
YY1 = int(np.min(my))
YY2 = int(np.max(my))
proyectiva = np.zeros((int(YY2-YY1),int(XX2-XX1),3))
imX=im.shape[0]
imY=im.shape[1]
for i in range(imX):
for j in range(imY):
txy = np.array([[j],[i],[1]])
txytemporal = np.dot(matH,txy)
px=int(txytemporal[0]/txytemporal[2])-XX1
py=int(txytemporal[1]/txytemporal[2])-YY1
if (px>0 and py>0 and py<YY2-YY1 and px<XX2-XX1):
proyectiva[py,px,:]=im[i,j,:]
return proyectiva, matH, im, (XX1, YY1)
def obtenerCoordenada(i,c):
coordenadasPuntos = getXYMouse(i, color= c);
punto= [];
punto.append((coordenadasPuntos[0,1], coordenadasPuntos[0,0]))
punto.append((coordenadasPuntos[1,1], coordenadasPuntos[1,0]))
punto.append((coordenadasPuntos[2,1], coordenadasPuntos[2,0] ))
punto.append((coordenadasPuntos[3,1], coordenadasPuntos[3,0]))
return punto;
def Interpolar(im,imo, h, lc):
print(lc[0])
imX=im.shape[0]
imY=im.shape[1]
imxx=imo.shape[0]
imyy=imo.shape[1]
h_inversa = np.linalg.inv(h)
for i in range(imX):
for j in range(imY):
if sum(im[i,j,:])==0:
txy = np.array([[j+lc[0]],[i+lc[1]],[1]])
t = np.dot(h_inversa,txy)
px=int(t[0]/t[2])
py=int(t[1]/t[2])
if (px>0 and py>0 and px<imyy and py<imxx):
im[i,j,:] = imo[py,px,:]
return im
if __name__ == '__main__':
origen= [];
destino= [];
#origen = [(220,110),(30,500),
# (375,95),(325,500)]
#destino = [(150,200),(150,700),
# (300,200),(300,700)]
ImagenProyectiva, H, imo, llc = TransformacionProyectiva("mural.jpg", origen, destino)
ImagenProyetivaMejorada = Interpolar(ImagenProyectiva, imo, H, llc)
misc.imsave("ImagenProyetivaMejorada.jpg",ImagenProyetivaMejorada)
5. Deep learning
Execution requirements
Visual studio 2017 Python 3.6 OpenCv Numpy PIL matplotlib scipy
Contributing and Feedback
Any ideas or feedback about this research?. Help me to improve it.
Authors
- Created by Ramses Alexander Coraspe Valdez
- Created on April, 2019
License
This project is licensed under the terms of the MIT license.